Accuplacer Math Prep
(from someone who can actually explain it)
Free Accuplacer practice tests & solution videos, or dig deeper with full topic review videos
You might not realize it, but the Accuplacer (or your state's version of it) is the most important test you'll ever take. It can add semesters or years to your education, possibly preventing you from completing your degree or transfer before life or work makes you give up on your dreams.
So before you do anything else, watch the video to the right and take this freaking test seriously! Chris is an experienced tutor with over 15 years experience tutoring math to students of all abilities and levels, in a way it actually makes sense to normal people.
| Free Accuplacer practice tests & solutions videos |
|---|
In-Depth Math Review:
Arithmetic
| Content Category | Skills | Example | Lessons |
|---|---|---|---|
| Operations with Integers | Order of operations, adding, subtracting, multiplying, and dividing basic integers | $72+4÷2+5$ | Intro to PEMDAS |
| Operations with Fractions | Adding, subtracting, multiplying, and dividing fractions | $2/3+(3/4×1/2)+(3/4-1/3)$ | Adding & Subtracting Fractions Multiplying & Dividing Fractions | Operations with Decimals | Adding,subtracting,multiplying,and dividing decimals | $7.46+1.85+2.5×3$ | Decimals Decimals rounding | Operations between mixed numbers and improper fractions | Adding, subtracting, multiplying,and dividing using mixed numbers and improper fractions | $7(1/2)+ 18.85+4(2/3)$ | Improper Fractions and Mixed Numbers | Exponents | Raising numbers to "a power" (how many times a number is multiplied by itself) | $2^4+3^2$ | Intro to Exponents Exponent Rules, Like Bases, & Negative Exponents Scientific Notation | Square Roots | A number that produces a specified quantity when multiplied by itself. | $√4+√81$ | Simplifying Roots & Radicals | Ratios and Proportions | "Part over whole" or fractions that equals a similar fraction | $X/2=12/8$ | Ratios & Proportions | Percentages | "A part" of a certain value which is used in operations. | 20% of 100 + 30% of 60 | Percents as Ratios Percent Increase & Decrease Percents As Decimals Hard Multi-Step Percent Problems | Averages | Another word for the "mean" which is a sum of all numbers in a set of data divided by the amount of numbers | Steve tried to compute the average of his 5 test scores. He scored 86 on one, 55 on the next one, then 99, 77, and 90. What is Steve's average test score? | Calculating The Mean (Average) | Geometry | Knowing both the area and the perimeter of triangles, quadrilaterals, and circles | If one angle of a triangle is 95 degrees and another is 35 degrees, what is the third angle of the triangle? | 180 Triangle Rule Problems Areas of Rectangles & Squares Rectangles & Squares Basic Circle Area Problems |
QAS: Quantitative Reasoning, Algebra, and Statistics
| Content Category | Skills | Example | Lessons |
|---|---|---|---|
| Substituting values for x | Being given a value for x and plugging in | What is the value at $(x^2-2)/(x-1)$ when x=2? | Intro to Variables & Expressions |
| Setting up an Equation | Translating an equation from words into numbers and variables | A car's distance is determined by the velocity multiplied by the amount of time the car is at that speed.If a car can go at a maximum velocity of 225 meters per second, what equation shows how far the car has travelled at its maximum speed? | How to Translate Words Into Equations | Operations with Polynomials | Adding,subtracting,multiplying,and dividing equations with multiple variables | Simplify: $2a+3b-(-6a+4b)$ | Adding Polynomials (a.k.a. Combining Like Terms) Distribution (a.k.a. "multiplying stuff out") Solving Equations With Distribution Basic FOIL on 2-by-2 parentheses | Factoring | Undoing a polynomial and simplifying it into its most basic equations as well as using it to find certain input values | What is one possible factor of $x^2+4x+3$ ? | Factoring Stuff Out (a.k.a. "distrubution in reverse") Easier Factoring Problems Factoring Difference of Squares Hard Factoring Problems | Linear Equations with One Variable | An input which leads to an output and using the output to solve for the input | Solve for x when $2(x-2)=-10$ | Solving Equations With Addition & Subtraction Only] Solving Equations With Multiplication & Division] Solving Two Step Equations | Exponent Properties | Multiplying, dviding, or taking the power of a number or variable to a power | $(x^2)((x^5)^2)/ x^9$ =? | Basic Exponent Rules & Rational Expressions Negative Exponents Common Algebraic Canceling Mistakes | Irrational functions and multiplying by the Complex Conjugate | Simplifying a polynomial over a polynomial and being able to simplify roots in a denominator. | $ √x/(3√x- √y)$ | Dividing Roots & Rationalizing Denominators Solving Rational Equations (x's in denominators) | System of Equations | Solving for an intersection point of two equation at a designated x or y value. | Solve for x and y: $2x+3y=6$ $8x-4y=-12$ | Solving Systems of Simultaneous Equations with Elimination Solving Systems of Simultaneous Equations with Substitution Solving 3 Simultaneous Equations with 3 Unknowns | Inequalities | Solving for the range of a functions x or y value using manipulation of a number line | What is the range of x for the function $2x+5<6$ ? | Solving "Linear" Inequalities |
Advanced Algebra and Functions
| Content Category | Skills | Example | Lessons | Complex Functions | Plugging in inputs for outputs and understanding their meaning including inequalities, a system of equations (more than one variable), exponential, and absolute value | A manufacturer for raw ore has one of two options for refining material: Process A or Process B. Procss A is $A(t)=2t^2+t$ and Process B is $20t$ with t being time in days. If the manufacturer has 7 days to refine ore, what is the maximum output possible? | Solving Messy Equations: Combining Like Terms Solving Systems of Simultaneous Equations with Elimination Absolute Value Equations Solving Inequalities with just X Graphing Exponentials Solving Exponential Equations Using Logs |
|---|---|---|---|
| Complex Exponents | Raising a number to a rational or irrational number or variable | Simplify the following: $(x^(1/2)) (y^(2/3))(z^(5/6))$ | Simplifying Roots & Radicals Rational Exponents (a.k.a. fractions upstairs) Basic Exponent Rules & Rational Expressions Common Algebraic Canceling Mistakes | Complex Numbers | Numbers which equal the square root of a negative number ($i$) | What is $i^24$ equal to? | Imaginary Numbers & Square Roots of Negatives Complex Numbers | Arithmatic and Geometric Sequences | A function which produces a series of numbers multiplied,divided, added, or subtracted by the previous terms | What is the next term in the geometric sequence 64,32,16,8...? | Geometric Sequences & Series Arithmetic Sequences & Series | Matrices | A set of numbers which can be added, subtracted, multiplied, and divided | [2 -6] - [-2 4]=? | Basic Matrix Operations Multiplying Matrices The Determinant |
| Angles | Using the degrees of an angle to solve for other angle values within a set of parallel lines, adjacent to the original angle, or "vertical" angles |
Solve for x:
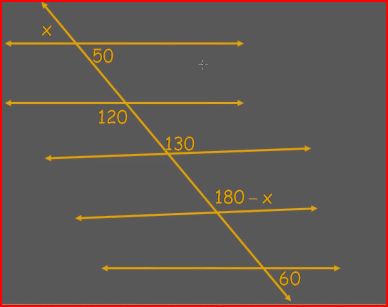
|
Parallel Lines & Transversals Theorems Parallel Lines & Transversals Problems |
| Triangles | An isosceles (two sides equal), equalateral (all sides equal), or scalene (no sides equal) 3-sided shape whose angles add up to 180 degrees |
Solve for x:
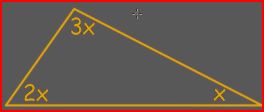
| Obtuse, Acute, and Right Triangles Scalene, Isosceles, and Equilateral Triangles 180Triangle Rule Problems Triangle Exterior Angle Theorem | Congruent Triangles and Pythagorean Theorem | Using congruent triangles to solve for the its angles and using the Pythagorean Theorem ($a^2+b^2=c^2$) |
Solve for x:
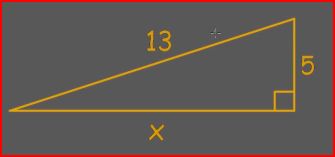
|
The Pythagorean Theorem Everything You Need To Know About Congruent Triangles Tips & Tricks For Congruent Triangle Proofs SSS, SAS, ASA, AAS, SSA, H-L/h3> | Circles | Using the radius and diameter to find the perimeter (circumference), area, and arc |
Calculate the arc of the given sector of the circle:
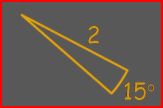
|
Circle Vocab Basic Circle Proofs Circumference & Diameter Basic Circle Area Problems Areas of Circle Sectors | Rectangles | A four-sided quadrilateral with two sets of equal sides |
Solve for x:
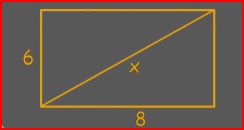
|
Areas of Rectangles & Squares Rectangles & Squares |
| Three-dimensional concepts | Taking the volume and surface area of shapes knowing information about the 2-D shape's area |
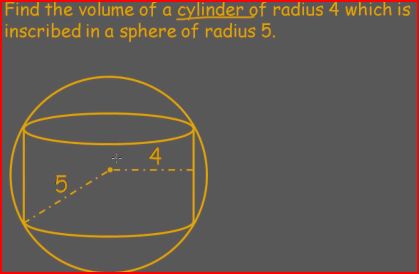
| Surface Area of 3-D Shapes Volume of Solids |
| Right-triangle Trigonometry and the Unit Circle | Using the degrees of an angle to solve for other angle values within a set of parallel lines, adjacent to the original angle, or "vertical" angles |
Calculate the missing sides:
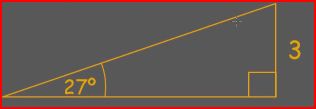
|
Intro to SohCahToa Solving Triangles The Unit Circle Introducing Secant, Co-Secant & Co-Tangent Inverse Trig Functions |
| Special Angles and Trig Identities | Special cases and equations involving SohCahToa | Simplify the following term: $sin(2x)$ | The Pythagorean Identity: sin2X + cos2X = 1 Proofs Using The "Other Two" Pythagorean Identities: tan2X+1 = sec2X & 1+cot2X = csc2X Double-Angle, Half-Angle, and Sum/Difference Formulas |