Making Trigonometry fun tolerable
Chris is a Stanford-educated tutor with over 10 years experience tutoring Trigonometry to students of all abilities, from students struggling to get from a C to a B, to go-getters trying to move an A- up to an A, to struggling students just hoping to pass. In that time he got a lot of experience learning how to explain this stuff in a way it actually makes sense to non-math people. Through his videos he has helped countless students, and he can do the same for you.
Trigonometry
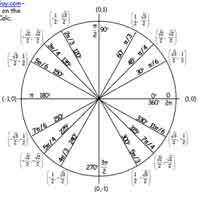
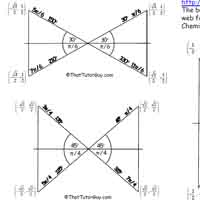
Click the thumbnail below to download a pdf of the Unit Circle for your trig class, in both radians and degrees. Also shown is the "bowtie angles" chart, which is a dumb name but really gets the point across: each angle on the unit circle has three buddies which have the same reference angle, so the sooner you recognize these virtual bowties the sooner you'll master the unit circle (and the sooner you can quit talking about bowties like some kind of dorky Bond villain).
Unit Circle Chart
|
Bowtie Angles Chart
|
|---|
I. SohCahToa & The Unit Circle
With this chapter we'll start trig off on the right foot -- triangles -- which has worked great for my tutoring students over the years. Also covered: what SohCahToa is (other than a weird abbreviation for the sinusoidal functions); what opposite, adjacent, and hypotenuse mean; how to find sine, cosine and tangent; and how to work a bunch of "solving triangles" problems.
In this chapter we'll get into the 30-60-90 and 45-45-90 triangles, with special emphasis on how to find their sides, do SohCahToa on them, and not get confused between which is which. Also, some super-tricky examples for students with tough teachers.
These new trig functions are just the reciprocal (flip) of sine, cosine and tangent, but they can be confusing, so we'll emphasize always writing them in the correct order each time, and we'll do lots of examples. I'll also show you how to do these on your calculator, which doesn't have buttons for these.
The longest chapter in trig. We'll start off slow, developing understanding by using SohCahToa to derive only the first quadrant of the unit circle at first. Then we'll work through reference angles, sign tricks, negative angles, co-terminal angles and undefined functions until you can calculate the six trig functions for any angle. We'll finish up with some tricks for memorizing the Unit Circle Chart.
Now that you've learned the Unit Circle in degrees, we're ready for Radians. This chapter the radian version of everything: reference angles in radians, negative angles in radians, etc. I also demonstrate common test problems like converting radians to degrees and degrees to radians, finding the six trig functions of angles with radians, and tricks for memorizing the radian unit circle.
Also called Arcsin, Arccos, Arctan, etc., these are problems like sin-1(1) where they give you the sin/cos/tan of an angle and you're supposed to give the angle in the correct quadrant. Key for solving trig equations, I explain how to do these with the unit circle or a calculator.
These are those problems where you've got sines and cosines inside of each other. Like you'll take "the inverse cosine of the sine of pi/3" or "the tangent of the inverse cotangent of 1". Very complicated looking, but if you work from inside out you can do these all day long.
II. Formulas, Equations & Identities
Trig equations are problems where you're solving for X or Theta but they're hidden behind a trig function, like "2sinX-1=0" or "tan2X-1=0". Lots of vocab in this one -- specific solutions, general solutions, 2npi, 360n -- and lots of factoring to do too. Easy to get confused between these and inverse trig functions!
Proofs strike fear in many a heart because most students were traumatized by proofs in Geometry. But have no fear. In this chapter I'll show you how to easily memorize the key identities you'll need, as well as take you through the Big Three techniques that will help you spot and solve most proofs.
Double-angle, half-angle, sum, difference, even-odd properties... I cover all the odds and ends here in one place. Most of these you'll never see again, so I focus on getting you through it quick so you can move on.
Two trig identities which reduce a sin^2 or cos^2 to first-order expressions, a key skill for calculus.
III. Graphing Trig Functions
These problems are frustrating for students because they pretty much all look the same, yet you can lose big points if you get one little shift or label wrong. Plus there's the annoying vocab: Amplitude, "b", phase shift, vertical shift. No worries, the videos in this chapter will sort it all out using explanations and techniques my students have found helpful, and I'll point out common errors to avoid.
I put these four in a separate chapter from Sine & Cosine for two reasons. First, many non-honors students don't even have to do these, so why scare you. Second, you should really get good at sine & cosine graphs first, since these four badboys are way easier if you base them on sine and cosine graphs, which is the approach I find helps students the most.
IV. Applications of Trig
Laws of Sines & Cosines
Basic Law of Sines problems
The Law of Sines "Ambiguous Case"
Law of Cosines
Earlier in Trig, we've already had a few videos about solving right triangles for missing sides, so how is this chapter different? It no longer has to be a right triangle! These problems are way more complicated than SohCahToa, yet in this chapter students often seem relieved to actually be "doing something" again rather than learning "a bunch of stuff you'll never see again".
Basics of vector addition, subtraction, multiplication, dot product, scalar product, magnitude, unit vectors, cross multiplication, and components.
This chapter covers converting parametric equations to rectangular and back again, eliminating the parameter, parametric forms of circles and ellipses, and graphing them.
This chapter covers kinematics projectile motion problems as you would see in Pre-Calculus or Algebra 2 math classes. This topic is covered in more depth on the physics page. One-dimensional and two-dimensional gravity problems, range, vector components of velocity, etc.
This chapter covers the basics of arc length and sector area, as well as difficult word problems about bike gears, vehicle speed, planets, and velocity of rotating objects.
This chapter covers everything from graphing polar coordinates and functions to converting equations between polar and Cartesian x-y coordinates. Also, how to do these on your calculator!